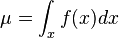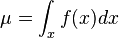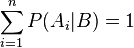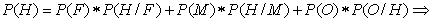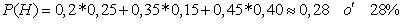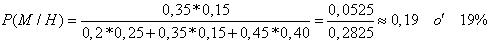domingo, 5 de mayo de 2013

BLOQUE 3 Calculo de la Media y la desviación Estandar

Calculo de la Media y la desviación Estandar


La desviación estándar o desviación típica (denotada con el símbolo σ o s, dependiendo de la procedencia del conjunto de datos) es una medida de centralización o dispersión para variables de razón (radio o cociente) y de intervalo, de gran utilidad en la estadística descriptiva.
Se define como la raíz cuadrada de la varianza. Junto con este valor, la desviación típica es una medida (cuadrática) que informa de la media de distancias que tienen los datos respecto de su media aritmética, expresada en las mismas unidades que la variable.
Para conocer con detalle un conjunto de datos, no basta con conocer las medidas de tendencia central, sino que necesitamos conocer también la desviación que presentan los datos en su distribución respecto de la media aritmética de dicha distribución, con objeto de tener una visión de los mismos más acorde con la realidad al momento de describirlos e interpretarlos para la toma de decisiones.



La desviación estándar es una medida del grado de dispersión de los datos con respecto al valor promedio. Dicho de otra manera, la desviación estándar es simplemente el "promedio" o variación esperada con respecto a la media aritmética.

La desviación estándar puede ser interpretada como una medida de incertidumbre. La desviación estándar de un grupo repetido de medidas nos da la precisión de éstas. Cuando se va a determinar si un grupo de medidas está de acuerdo con el modelo teórico, la desviación estándar de esas medidas es de vital importancia: si la media de las medidas está demasiado alejada de la predicción (con la distancia medida en desviaciones estándar), entonces consideramos que las medidas contradicen la teoría. Esto es coherente, ya que las mediciones caen fuera del rango de valores en el cual sería razonable esperar que ocurrieran si el modelo teórico fuera correcto. La desviación estándar es uno de tres parámetros de ubicación central; muestra la agrupación de los datos alrededor de un valor central (la media o promedio).

Distribución de probabilidad continua
Es posible calcular la desviación estándar de una variable aleatoria continua como la raíz cuadrada de la integral

{\sigma}^2 = \int_{(x - \mu)}^2 f(x) dx

donde: \mu = \int_{x} f(x) dx

Distribución de probabilidad discreta
La DS es la raíz cuadrada de la varianza de la distribución de probabilidad discreta

s^2 = \frac{1}{n} \sum_{i=1}^n \left( x_i - \overline{x} \right) ^ 2

Así la varianza es la media de los cuadrados de las diferencias entre cada valor de la variable y la media aritmética de la distribución.

También hay otra función más sencilla de realizar y con menos riesgo de tener equivocaciones :

s^2 = \frac{ \sum_{i=1}^n x_i^2 - n\overline{x}^2}{n-1}

EJERCICIOS.

1.- Los pesos ( en libras ) de una muestra de cinco cajas enviadas por el servicio de mensajería UPS es :
              12       6       7       3       10  
a) Obtenga la amplitud de variación
       12  -  3  =  9
b)  Calcule la desviación media


c)  Determine la desviación estándar



2.-Las edades de una muestra de turistas canadienses que vuelan de Toronto a Hong Kong, fueron :
   32       21       60       47       54      17       72       55       33       41

a)  Calcule la amplitud de variación


b)  Determine la desviación media


c)  Evalúe la desviación estándar 


3.- 



4.- 


5.
- 

6.
- 

7.- 

8.-
 

9.-
 

10.- 




Publicado por en No hay comentarios:

BLOQUE 3 Función de la Probabilidad para una variable Discreta.

Función de la Probabilidad para una variable Discreta.
ESPACIO MUESTRAL. El conjunto de todos los resultados posibles de un experimento estadístico 
denotado por “S” o “Ω ” 
VARIABLE. Se denomina variable a la entidad que puede tomar un valor cualesquiera durante la 
duración de un proceso dado. Si la variable toma un solo valor durante el proceso se llama constante. 
VARIABLE ALEATORIA: Es una función que asocia un número real a cada elemento del espacio 
muestral. Es decir son aquellas que pueden diferir de una respuesta a otra. 

Una variable aleatoria se puede clasificar en: 
  •  Variable aleatoria discreta. 
  • Variable aleatoria continua. 



Variable aleatoria discreta. Una variable discreta proporciona datos que son llamados datos cuantitativos discretos y son respuestas numéricas que resultan de un proceso de conteo. 

La cantidad de alumnos regulares en un grupo escolar. 
El número de águilas en cinco lanzamientos de una moneda. 
Número de circuitos en una computadora. 
El número de vehículos vendidos en un día, en un lote de autos 

Variable aleatoria continua. Es aquella que se encuentra dentro de un intervalo comprendido entre dos 
valores cualesquiera; ésta puede asumir infinito número de valores y éstos se pueden medir.

La estatura de un alumno de un grupo escolar. 
El peso en gramos de una moneda. 
La edad de un hijo de familia. 
Las dimensiones de un vehículo.


EJERCICIOS.

1.-Sea X la variable aleatoria que representa la demanda semanal de una maquina de premios que esta puesta en un supermercado. La función de probabilidad para Z esta dada por,

         
F(x)=  x2-3x                             para x= 4, 5, 6, 7
              60                                  si x= 4, 5, 6, 7
Encuentre, a) la distribución acumulada, b) la desviación estándar,



 Función de Probabilidad
X
4
5
6
7
P (Xi)
4/60
10/60
18/60
28/60



P(X=4)= (4)2-3/4) = 4/60                        
                    60
P(X=5)= (5)2-3/5) = 10/60
                    60
P(X=6)= (6)2-3/6) = 18/60
                    60
P(X=7)= (7)2-3/7) = 28/60
                    60

Función de Distribución Acumulada
X
P(X)
F(X)
4
4/60
0+4/60 = 4/60
5
10/60
4/60+10/60 = 14/60
6
18/60
14/60+18/60 = 32/60
7
28/60
32/60+28/60 = 1
Media
µ = (4) (4/60) + (5) (10/60) + (6) (18/60) (7) (28/60) = 37/60
Varianza
V(x)= (4 - 37/60)2(4/60) + (5 – 37/60)2 (10/60) + (6 – 37/60)2 (18/60) + (7 – 37/60) (28/60)
V(x)=8.560
Desviación Estándar
σ =    (8.560)1/2    = 2.925

2.-De los usuarios de un centro de documentaci on, el 23 % pertenece al grupo I de edad (menos de 20 años). Supongamos, tambi en, que la poblaci on es su cientemente grande como para que al elegir un usuario al azar y apartarlo, no se altere dicho porcentaje. Realizamos el experimento que consiste en elegir al azar tres usuarios del centro de documentaci on y observar la variable aleatoria X=n umero de usuarios que pertenecen al grupo I de edad, entre los tres elegidos al azar.
a) Hallar el conjunto de los posibles resultados de la variable aleatoria X, as como su funci on de probabilidad.
b) Hallar la probabilidad de que el n umero de usuarios que pertenecen al grupo I sea menor que dos.
c) Determinar la funci on de distribuci on de X y hacer su representaci on gr a ca.
d) Calcular la media y la desviaci on t pica de X.


3.-De un total de 500 libros, 50 son cient cos. Extraemos al azar un primer libro entre los 500 y lo reponemos en la poblaci on de libros antes de realizar una nueva extracci on; volvemos a extraer al azar un segundo libro entre los 500 y lo reponemos antes de hacer una nueva extracci on; nuevamente, extraemos un quinto libro entre los 500. Consideramos la variable aleatoria X=n umero de libros cient cos, entre los 5 elegidos al azar con reposici on.
a) Hallar la funci on de probabilidad de X y hacer su representaci on gr a ca.
b) Determinar la funci on de distribuci on de X y hacer su representaci on gr a ca.
c) A partir de la funci on de distribuci on de X, calcular la probabilidad de que el n umero de libros cient cos sea mayor que 3.
d) Calcular la media y la desviaci on t pica de X.



4.-Los libros que salen de una imprenta se clasi can en defectuosos (si tienen defectos de impresi on) y no defectuosos (si no tienen defectos de impresi on). Se supone que la cantidad de libros que salen de dicha imprenta es tan grande, que puede considerarse in nita. Por tanto, si elegimos y apartamos un libro, esto no altera el porcentaje de libros no defectuosos, que es 95 %.
a) Si se eligen al azar 20 libros, >cu al es la probabilidad de que 18 de ellos sean no defectuosos?
b) Si se eligen al azar 25 libros, >cu al es la probabilidad de que el n umero de libros no defectuosos sea mayor o igual que 21?



5.-  Se sabe que el 4 % de los libros que se prestan en una biblioteca escolar se devuelven con retraso. Se realiza el experimento que consiste en observar si la devoluci on de cada libro se ha hecho con retraso o no. Se eligen al azar 12 libros prestados.
a) >Cu al es la probabilidad de que se devuelvan con retraso 2 libros?
b) >Cu al es la probabilidad de que se devuelvan con retraso m as de 2 libros?

6.- Supongamos que el 1 % de la poblaci on de todos los usuarios de un centro de documentaci on tiene menos de 10 años. Supongamos, tambi en, que la poblaci on es su cientemente grande como para que al elegir un usuario al azar y apartarlo, no se altere dicho porcentaje. Se eligen al azar 15 usuarios de dicho centro de documentaci on. Calcular:Dra. Josefa Mar n Fern andez. Grado en Informaci on y Documentaci on. Estad stica. 
a) La probabilidad de que ninguno de ellos tenga menos de 10 a~nos.
b) La probabilidad de que tengan menos de 10 años 3 usuarios o menos.
c) La probabilidad de que tengan menos de 10 años menos de 3 usuarios.
d) La probabilidad de que tengan menos de 10 años m as de 2 usuarios.
e) La probabilidad de que tengan menos de 10 años 2 usuarios o m as.
f) La probabilidad de que el n umero de usuarios con menos de 10 años est e comprendida entre 2 (incluido) y 10 (incluido).
g) El n umero medio de usuarios con menos de 10 años.


7.-

9.- Sea el experimento aleatorio de averiguar la marca de tabaco que preferirá un individuo entre las posibles marcas: <<X>>, <<Y>>, <<Z>>.
En este caso la asociación de un número para cada suceso elemental posible del experimento no es inmediata. En consecuencia, se establece una correspondencia entre el conjunto de los sucesos elementales posibles y el conjunto de los números reales, del modo siguiente:
Al suceso elemental <<preferir la marca X>> se le hace corresponder el número 1; al suceso elemental <<preferir la marca Y>> se le hace corresponder el número 2; al suceso elemental <<preferir la marca Z>> se le hace corresponder el número 3.
La variable aleatoria X será: X = (1,2,3).

Monografias.com

10.
-



Publicado por en No hay comentarios:

BLOQUE 3 Esperanza Matematica

ESPERANZA MATEMATICA.


La esperanza matemática o valor esperado de una variable aleatoria discreta es la suma del producto de la probabilidad de cada suceso por el valor de dicho suceso.

media
Los nombre de esperanza matemática y valor esperado tienen su origen en los juegos de azar y hacen referencia a la ganancia promedio esperada por un jugador cuando hace un gran número de apuestas.
Si la esperanza matemática es cero, E(x) = 0, el juego es equitativo, es decir, no existe ventaja ni para el jugador ni para la banca.



EJERCICIOS.
1.-Si una persona compra una papeleta en una rifa, en la que puede ganar de 5.000 € ó un segundo premio de 2000 € con probabilidades de: 0.001 y 0.003. ¿Cuál sería el precio justo a pagar por la papeleta?
E(x) = 5000 · 0.001 + 2000 · 0.003 = 11 €


2.-Un jugador lanza dos monedas. Gana 1 ó 2 € si aparecen una o dos caras. Por otra parte pierde 5 € si no aparece cara. Determinar la esperanza matemática del juego y si éste es favorable.
E = {(c,c);(c,x);(x,c);(x,x)}
p(+1) = 2/4
p(+2) = 1/4
p(−5) = 1/4
E(x)= 1 · 2/4 + 2 · 1/4 - 5 · 1/4 = −1/4. Es desfavorable

3.-En una ciudad, la temperatura máxima durante el mes de junio está distribuida normalmente con una media de 26º y una desviación típica de 4º. 
Calcular el número de días que se "espera", tengan temperatura máxima comprendida entre 22º y 28º.

Como se trata de una distribución Normal, tipificamos (estandarizamos) los valores 22 y 28: 
z1= (22 – 26) / 4 = -1
z2 = (28 – 26) / 4 = 0, 5
Entonces la probabilidad de que en un día de junio la temperatura máxima esté entre 22 y 28º es: 
p( 22< x < 28) = p( -1 < z < 0,5 ) = 0, 5328
Y el número esperado (esperanza) de días es: 
E(x) = n * p = 30 * 0, 5328 ≈ 16 días

4.-

5.
-

6.-



7.-
8.-

9.-

10.-

11.-

12
Publicado por en No hay comentarios:

BLOQUE 3 Teorema de Bayes


Teorema de Bayes.
En la teoría de la probabilidad el teorema de Bayes es un resultado enunciado por Thomas Bayes en 17631 que expresa la probabilidad condicional de un evento aleatorio A dado B en términos de la distribución de probabilidad condicional del evento B dado A y la distribución de probabilidad marginalde sólo A.
En términos más generales y menos matemáticos, el teorema de Bayes es de enorme relevancia puesto que vincula la probabilidad de A dado B con la probabilidad de B dado A. Es decir que sabiendo la probabilidad de tener un dolor de cabeza dado que se tiene gripe, se podría saber (si se tiene algún dato más), la probabilidad de tener gripe si se tiene un dolor de cabeza, muestra este sencillo ejemplo la alta relevancia del teorema en cuestión para la ciencia en todas sus ramas, puesto que tiene vinculación íntima con la comprensión de la probabilidad de aspectos causales dados los efectos observados.

Fórmula de Bayes

Con base en la definición de Probabilidad condicionada, obtenemos la Fórmula de Bayes, también conocida como la Regla de Bayes:

P(A_i|B) = \frac{P(B | A_i) P(A_i)}{\sum_{k=1}^n P(B | A_k) P(A_k)}

Aplicaciones

El teorema de Bayes es válido en todas las aplicaciones de la teoría de la probabilidad. Sin embargo, hay una controversia sobre el tipo de probabilidades que emplea. En esencia, los seguidores de la estadística tradicional sólo admiten probabilidades basadas en experimentos repetibles y que tengan una confirmación empírica mientras que los llamados estadísticos bayesianos permiten probabilidades subjetivas. El teorema puede servir entonces para indicar cómo debemos modificar nuestras probabilidades subjetivas cuando recibimos información adicional de un experimento. La estadística bayesiana está demostrando su utilidad en ciertas estimaciones basadas en el conocimiento subjetivo a priori y el hecho de permitir revisar esas estimaciones en función de la evidencia empírica es lo que está abriendo nuevas formas de hacer conocimiento. Una aplicación de esto son losclasificadores bayesianos que son frecuentemente usados en implementaciones de filtros de correo basura o spam, que se adaptan con el uso.

 Como observación, se tiene \sum_{i=1}^{n}P(A_i |B)=1y su demostración resulta trivial.


EJERCICIOS.


 

EJEMPLO 5
En la sala de pediatría de un hospital, el 60% de los pacientes son niñas. De los niños el 35% son menores de 24 meses. El 20% de las niñas tienen menos de 24 meses. Un pediatra que ingresa a la sala selecciona un infante al azar.
a. Determine el valor de la probabilidad de que sea menor de 24 meses.
b. Si el infante resulta ser menor de 24 meses. Determine la probabilidad que sea una niña.
SOLUCIÓN:
Se definen los sucesos:
Suceso H: seleccionar una niña.
Suceso V: seleccionar un niño.
Suceso M: infante menor de 24 meses.
En los ejercicios de probabilidad total y teorema de bayes, es importante identificar los sucesos que forman la población y cuál es la característica que tienen en común dichos sucesos. Estos serán los sucesos condicionados.
a. En este caso, la población es de los infantes. Y la característica en común es que sean menores de 24 meses. Por lo tanto, la probabilidad de seleccionar un infante menor de 24 meses es un ejemplo de probabilidad total. Su probabilidad será:

b. Para identificar cuando en un ejercicio se hace referencia al teorema de bayes, hay que partir de reconocer esta es una probabilidad condicionada y que la característica común de los sucesos condicionantes ya ha ocurrido. Entonces, la probabilidad de que sea niña una infante menor de 24 meses será:
EJEMPLO 6
Un médico cirujano se especializa en cirugías estéticas. Entre sus pacientes, el 20% se realizan correcciones faciales, un 35% implantes mamarios y el restante en otras cirugías correctivas. Se sabe además, que son de genero masculino el 25% de los que se realizan correcciones faciales, 15% implantes mamarios y 40% otras cirugías correctivas. Si se selecciona un paciente al azar, determine:
a. Determine la probabilidad de que sea de género masculino
b. Si resulta que es de género masculino, determine la probabilidad que se haya realizado una cirugía de implantes mamarios.
SOLUCIÓN:
Se definen los sucesos:
Suceso F: pacientes que se realizan cirugías faciales
Suceso M: pacientes que se realizan implantes mamarios
Suceso O: pacientes que se realizan otras cirugías correctivas
Suceso H: pacientes de género masculino
a. La probabilidad de que sea de género masculino se refiere a un problema de probabilidad total, ya que es el suceso condicionado y las cirugías los condicionantes. Dicho valor será:
b. Como el suceso condicionado ha ocurrido entonces se aplica el teorema de bayes, luego, el valor de la probabilidad será:
EJEMPLO 7
Un Doctor dispone de tres equipos electrónicos para realizar ecosonogramas. El uso que le da a cada equipo es de 25% al primero, 35% el segundo en y 40% el tercero. Se sabe que los aparatos tienen probabilidades de error de 1%, 2% y 3% respectivamente. Un paciente busca el resultado de una ecografía y observa que tiene un error. Determine la probabilidad de que se ha usado el primer aparato.
SOLUCIÓN:
Se definen los sucesos:
Suceso P: seleccionar el primer aparato
Suceso S: seleccionar el segundo aparato
Suceso T: seleccionar el tercer aparato
Suceso E: seleccionar un resultado con error
Se puede observar que la pregunta es sobre determinar la probabilidad de que un examen errado sea del primer aparato, es decir, ya ha ocurrido el error. Por lo tanto, debemos recurrir al teorema de bayes. Claro está, que es necesario de igual forma obtener la probabilidad de que los aparatos produzcan un resultado erróneo, por lo tanto:











Publicado por en No hay comentarios:
Suscribirse a: Entradas (Atom)